Curvature is common in business relationships: marketing spend shows diminishing returns, prices scale sublinearly with size, and operational outcomes vary nonlinearly over the day. This chapter shows how to model such patterns primarily with ordinary least squares (OLS) using transformations, low-order polynomials, and piecewise linear specifications. Advanced methods are briefly surveyed at the end.
Upon concluding this chapter, readers will be equipped with the skills to:
AmesHousing::make_ames() to obtain a cleaned, single-table versionggplot2::diamonds and ggplot2::mpg
readr::read_csv("Advertising.csv")
ISLR2::Wage
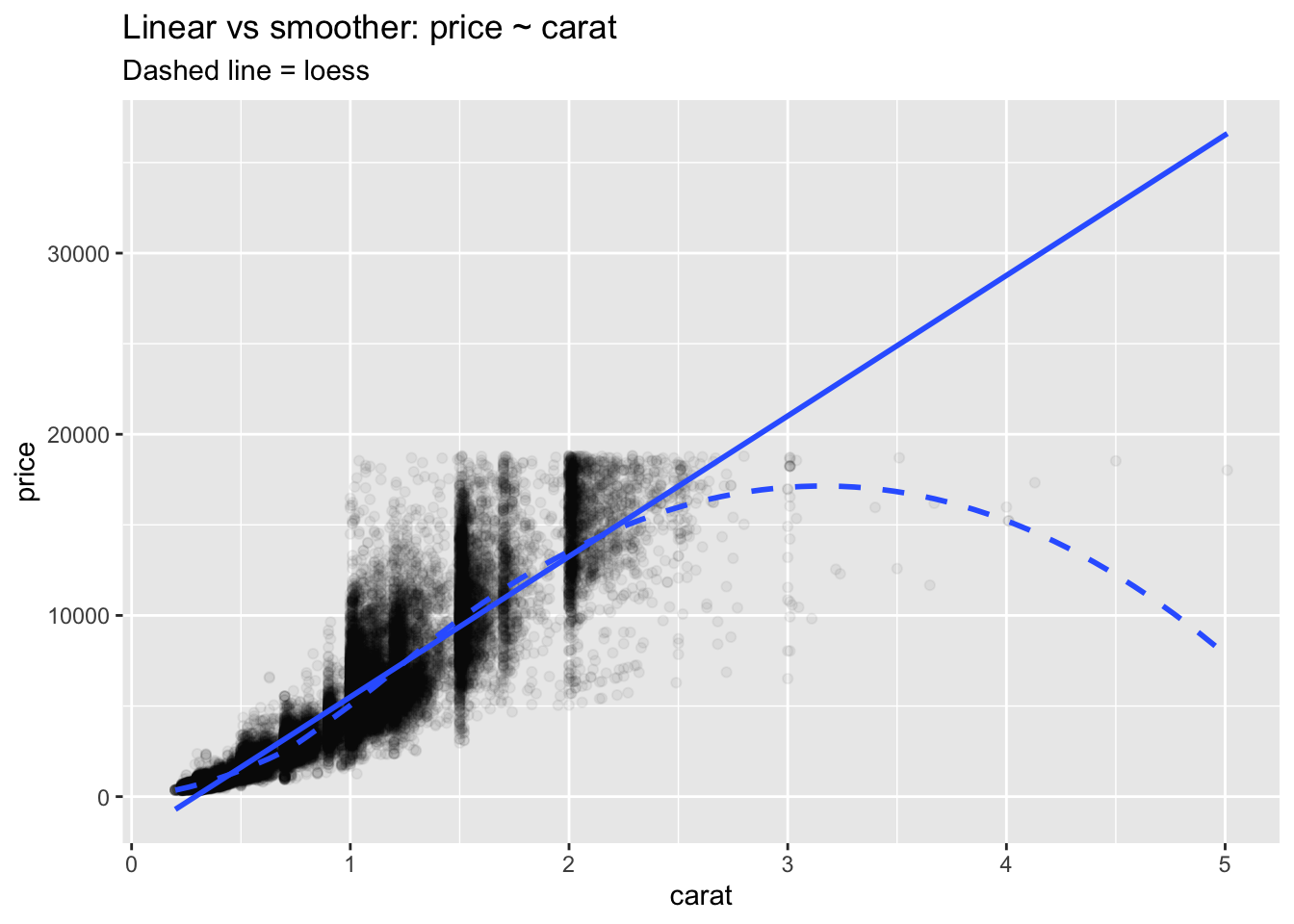
listings.csv.gz from the data portalday.csv and hour.csv from the repositorynycflights13::flights provides CC0 flight recordsAnscombe’s reminder: identical summaries can mask very different shapes. Always visualize.
# Visual comparison of linear fit vs flexible smoother (power-law context)
ggplot(diamonds, aes(carat, price)) +
geom_point(alpha = 0.05) +
geom_smooth(method = "lm", se = FALSE) +
geom_smooth(method = "loess", se = FALSE, linetype = "dashed") +
labs(title = "Linear vs smoother: price ~ carat", subtitle = "Dashed line = loess")`geom_smooth()` using formula = 'y ~ x'
`geom_smooth()` using formula = 'y ~ x'
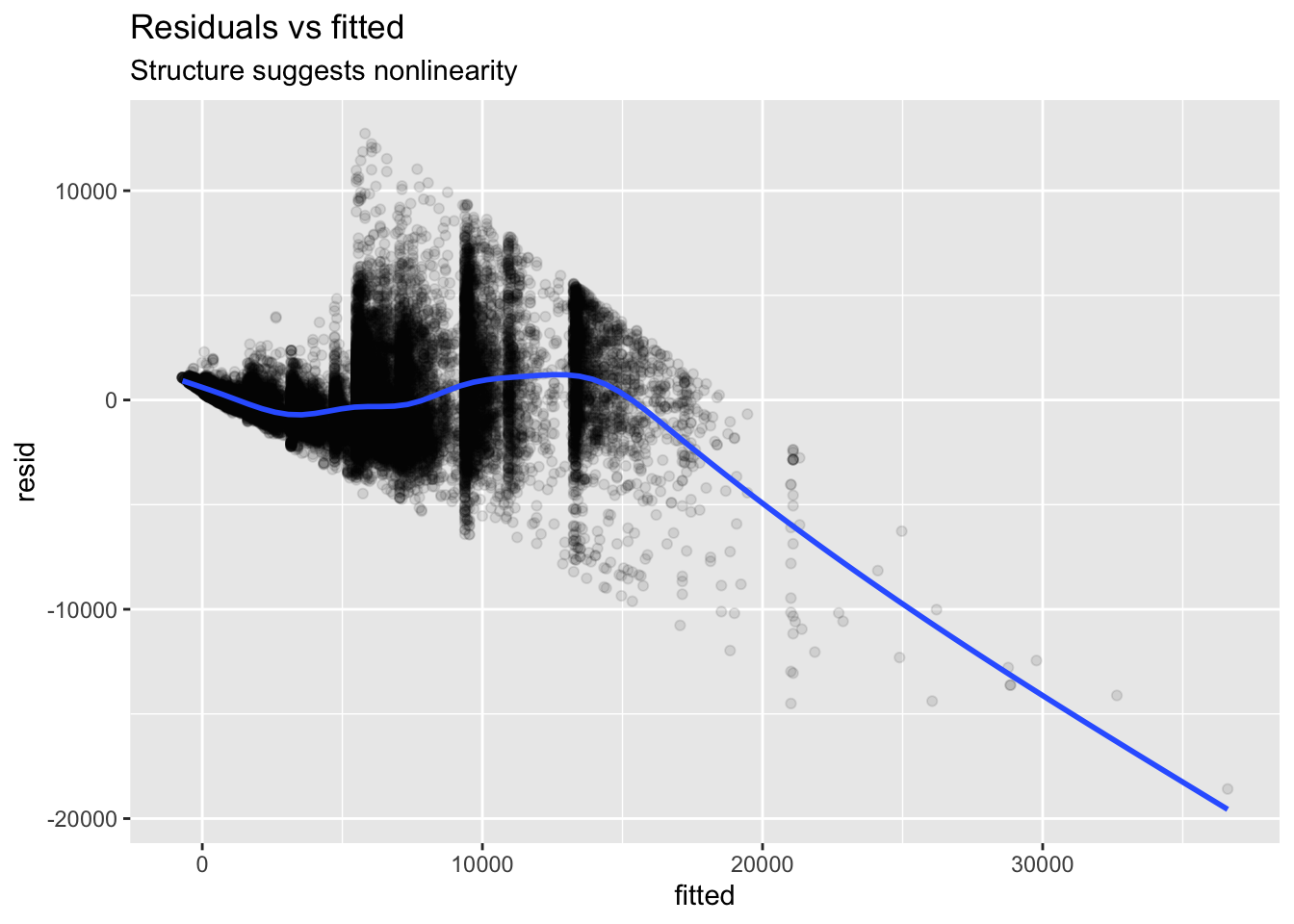
Residual patterns often reveal missed curvature.
`geom_smooth()` using method = 'gam' and formula = 'y ~ s(x, bs = "cs")'
Start with managerial meaning (absolute vs percent changes), then prefer the simplest form that removes residual structure.
Visualize → try simple transforms → consider low-order polynomials → justify knots for piecewise models → validate
Let \(Y\) be the outcome and \(X\) a single predictor. Derivatives and elasticities are evaluated at a given \(X\) with predicted \(Y\).
| Model | Specification | Slope \(dY/dX\) | Elasticity \(\frac{dY}{dX}\frac{X}{Y}\) | Managerial interpretation |
|---|---|---|---|---|
| Linear | \(Y=\beta_0+\beta_1 X+\varepsilon\) | \(\beta_1\) | \(\beta_1 \cdot X/Y\) | One-unit increase in \(X\) changes \(Y\) by \(\beta_1\) units |
| Linear–log | \(Y=\beta_0+\beta_1 \ln X+\varepsilon\) | \(\beta_1/X\) | \((\beta_1/X)\cdot X/Y=\beta_1/Y\) | 1% increase in \(X\) changes \(Y\) by \(\beta_1/100\) units |
| Log–linear | \(\ln Y=\beta_0+\beta_1 X+\varepsilon\) | \(\beta_1 Y\) | \(\beta_1 X\) | One-unit increase in \(X\) changes \(Y\) by \(100\cdot \beta_1\%\) |
| Log–log | \(\ln Y=\beta_0+\beta_1 \ln X+\varepsilon\) | \(\beta_1 Y/X\) | \(\beta_1\) | Elasticity of \(Y\) w.r.t. \(X\) equals \(\beta_1\) (constant) |
| Quadratic | \(Y=\beta_0+\beta_1 X+\beta_2 X^2+\varepsilon\) | \(\beta_1+2\beta_2 X\) | \((\beta_1+2\beta_2 X)\cdot X/Y\) | Turning point at \(X^{\star} =-\beta_1/(2\beta_2)\) if \(\beta_2<0\) |
Diamonds (retail pricing): price vs carat
Source: ggplot2::diamonds
Call:
lm(formula = log(price) ~ log(carat), data = diamonds)
Residuals:
Min 1Q Median 3Q Max
-1.50833 -0.16951 -0.00591 0.16637 1.33793
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 8.448661 0.001365 6190.9 <2e-16 ***
log(carat) 1.675817 0.001934 866.6 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.2627 on 53938 degrees of freedom
Multiple R-squared: 0.933, Adjusted R-squared: 0.933
F-statistic: 7.51e+05 on 1 and 53938 DF, p-value: < 2.2e-16Ames Housing (real estate pricing): sale price vs living area
Source: De Cock (2011), JSE; available via the AmesHousing package
Call:
lm(formula = log(Sale_Price) ~ log(Gr_Liv_Area), data = ames)
Residuals:
Min 1Q Median 3Q Max
-2.0778 -0.1465 0.0264 0.1740 0.8602
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.43019 0.11644 46.63 <2e-16 ***
log(Gr_Liv_Area) 0.90781 0.01602 56.66 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.2816 on 2928 degrees of freedom
Multiple R-squared: 0.523, Adjusted R-squared: 0.5228
F-statistic: 3210 on 1 and 2928 DF, p-value: < 2.2e-16ISLR Advertising: Sales ~ log(TV) (extend to other channels as needed)
Source: ISLR website (Advertising.csv)
New names:
• `` -> `...1`
Call:
lm(formula = sales ~ log(TV), data = adv)
Residuals:
Min 1Q Median 3Q Max
-5.9318 -2.6777 -0.2758 2.1227 9.2654
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -4.2026 1.1623 -3.616 0.00038 ***
log(TV) 3.9009 0.2432 16.038 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 3.45 on 198 degrees of freedom
Multiple R-squared: 0.565, Adjusted R-squared: 0.5628
F-statistic: 257.2 on 1 and 198 DF, p-value: < 2.2e-16ISLR Wage: log(wage) ~ age + age² (optionally add tenure, education)
Source: ISLR2::Wage
Call:
lm(formula = log(wage) ~ age + I(age^2), data = Wage)
Residuals:
Min 1Q Median 3Q Max
-1.72742 -0.19431 0.00655 0.18995 1.13251
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.468e+00 6.810e-02 50.93 <2e-16 ***
age 5.166e-02 3.232e-03 15.98 <2e-16 ***
I(age^2) -5.202e-04 3.685e-05 -14.12 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.3325 on 2997 degrees of freedom
Multiple R-squared: 0.1069, Adjusted R-squared: 0.1063
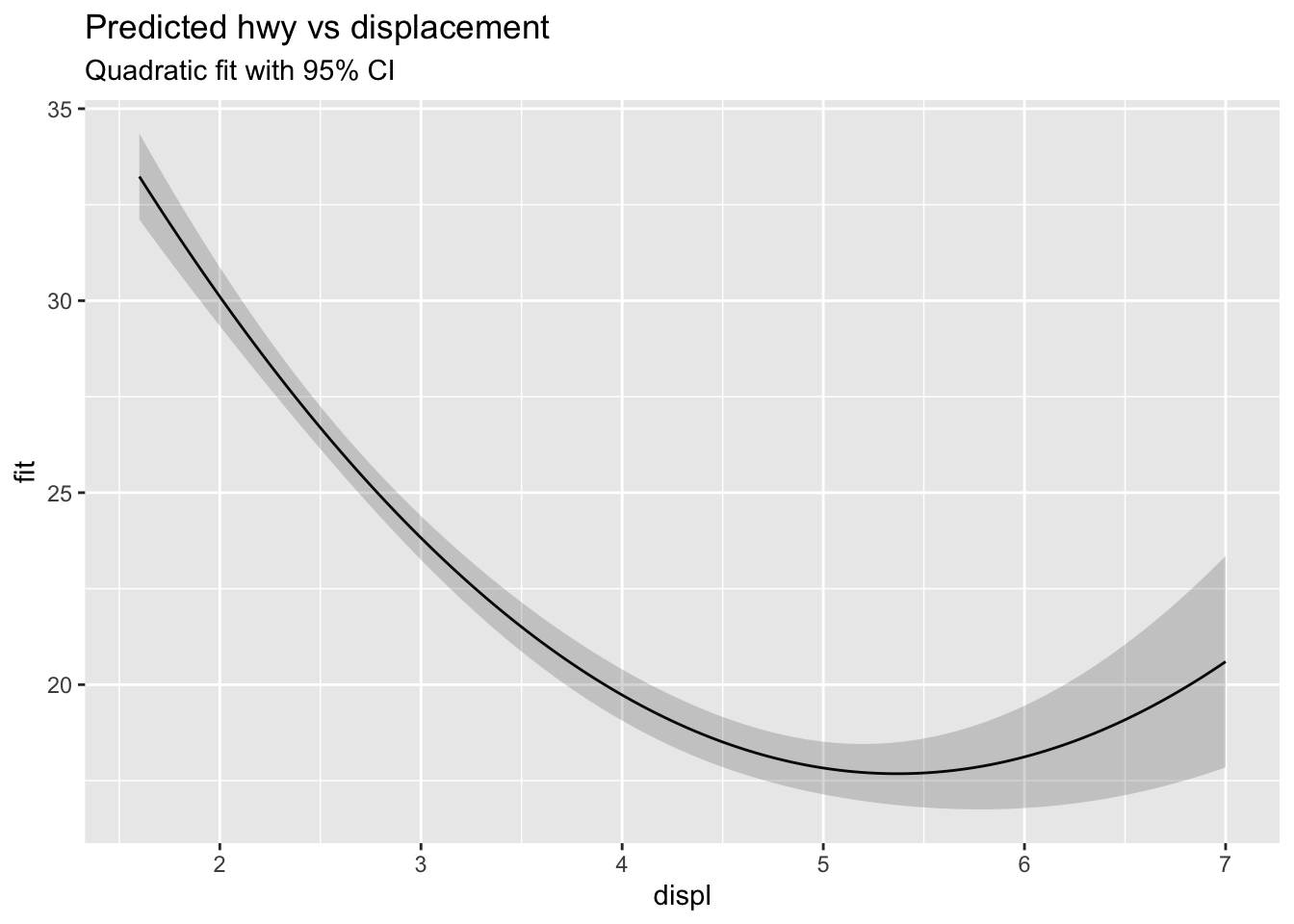
F-statistic: 179.3 on 2 and 2997 DF, p-value: < 2.2e-16Automotive fuel economy: hwy ~ displ + displ²
Source: ggplot2::mpg
displ
5.367878 Bike demand vs temperature (UCI Bike Sharing): cnt ~ temp + temp²
Download day.csv from the UCI repository and place at data/bike_day.csv
Source: UCI Machine Learning Repository (Bike Sharing Dataset)
NYC Taxi: total fare vs distance with base fee and per-mile segments. Use a sampled trips file (e.g., data/nyc_taxi_sample.csv) and the official rate card to justify the knot(s)
Source: NYC Taxi & Limousine Commission trip records; NYC TLC rate card
USPS shipping: postage vs weight shows step/tier pricing (use hinges at ounce thresholds)
Source: USPS Notice 123
# usps <- tribble(
# ~weight_oz, ~price_usd,
# 1, 0.68,
# 2, 0.92,
# 3, 1.16,
# 3.5, 1.40
# )
# usps <- usps %>% mutate(after1 = pmax(weight_oz - 1, 0),
# after2 = pmax(weight_oz - 2, 0),
# after3 = pmax(weight_oz - 3, 0))
# m_hinge_usps <- lm(price_usd ~ weight_oz + after1 + after2 + after3, data = usps)
# summary(m_hinge_usps)Airline operations: departure delay vs hour (nycflights13). Splines provide a compact, smooth alternative to high-order polynomials
Source: nycflights13 package (CC0)
Call:
lm(formula = dep_delay ~ bs(hour, df = 4), data = fl)
Residuals:
Min 1Q Median 3Q Max
-66.09 -18.26 -9.49 -1.03 1296.23
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.3436 0.4035 0.852 0.394
bs(hour, df = 4)1 3.2272 0.7622 4.234 2.3e-05 ***
bs(hour, df = 4)2 7.0820 0.5462 12.966 < 2e-16 ***
bs(hour, df = 4)3 32.5465 0.7685 42.349 < 2e-16 ***
bs(hour, df = 4)4 16.3872 0.6992 23.436 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 39.38 on 328516 degrees of freedom
Multiple R-squared: 0.04081, Adjusted R-squared: 0.0408
F-statistic: 3494 on 4 and 328516 DF, p-value: < 2.2e-16Visualize effect curve with confidence band for any fitted model
newx <- tibble(displ = seq(min(mpg$displ), max(mpg$displ), length.out = 200))
preds <- cbind(newx, predict(m_quad_mpg, newdata = newx, interval = "confidence"))
ggplot(preds, aes(displ, fit)) +
geom_line() +
geom_ribbon(aes(ymin = lwr, ymax = upr), alpha = 0.2) +
labs(title = "Predicted hwy vs displacement", subtitle = "Quadratic fit with 95% CI")
Solar PV learning curve: log(price_per_watt) ~ log(cumulative_capacity)
Download OWID series and join to create solar_df with columns price_watt, cum_capacity
Source: Our World in Data
set.seed(123)
idx <- sample.int(nrow(mpg), size = floor(0.8 * nrow(mpg)))
m_train <- mpg[idx, ]; m_test <- mpg[-idx, ]
m_lin_mpg <- lm(hwy ~ displ, data = m_train)
m_quad_mpg <- lm(hwy ~ displ + I(displ^2), data = m_train)
rmse <- function(y, yhat) sqrt(mean((y - yhat)^2))
rmse_lin <- rmse(m_test$hwy, predict(m_lin_mpg, newdata = m_test))
rmse_quad <- rmse(m_test$hwy, predict(m_quad_mpg, newdata = m_test))
tibble(model = c("linear","quadratic"), rmse = c(rmse_lin, rmse_quad))For pricing and demand, log–log elasticities communicate clearly. For costs, linear or linear–log forms often align with managerial expectations
Implementation of these advanced methods is beyond the scope of this chapter; use them as benchmarks when OLS forms clearly underfit